Question

Jason takes off across level water on his jet-powered skis. The combined mass of Jason and skis is 75 kg (the mass of the fuel is negligible). The skis have a thrust of 200 N and a coefficient of kinetic friction on water of 0.1. Unfortunately, the skis run out of fuel after only 41 s. How far has Jason traveled when he finally coasts to a stop?

Answer 1

r = 3858.7635 m

Step-by-step explanation:

first we will use the law of newton as:

-mg+N = 0

N = mg

where m is the mass, g the gravity and N is the normal force, So:

N = (75)(9.8)

N = 735

also, when the skis had fuel:

F-
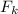`F_k` = ma

where F is the force of the skis,
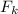`F_k` is the force by the kinetic friction and a is the aceleration.

so:

F-
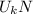`U_kN` = ma

200N-(0.1)(735) = (75)a

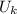`U_k` is the coefficient of kinetic friction on water, therefore solving for a:

a = 1.687 m/s^2

so, with the aceleration we can find the velocity V of jason just after the skis run out of fuel as:

V = at

V = (1.687m/s^2)(41s)

V = 69.167 m/s^2

Where t is the time in which the skis run out of fuel. Now using the law of the conservation of energy we will find the distance as:

Initial Energy - Final Energy = Work of Friction

`(1)/(2)MV^2 = U_kNd`

`(1)/(2)(75)(69.167)^2 = (0.1)(735)d`

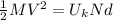
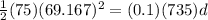
d = 2440.8m

that means that jason traveled 2440.8m after the skis run out of fuel.

Additionally, the distance x that jason traveled with fuel is calculated as:

x =
`(1)/(2)at^2`

x =
`(1)/(2)(1.687)(41)^2`

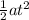
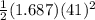
x = 1417.9235 m

Finally, Jason travel 3858.76 m when he finally coast to a stop. It is calculated as:

r = x + d

r = 1417.9235+2440.8

r = 3858.7635 m