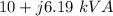Question

In the circuit below, the impedance Z1 dissipates 10 kW with a power factor of 0.85 lagging. Z2 draws 12 kVA apparent power with a power factor of 0.75 leading. The frequency of the source is 60 Hz.

Answer 1

The impedance Z₁ is
`10+j6.19\ kVA`

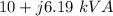
Step-by-step explanation:

Given that,

Dissipates power = 10 kW

Power factor = 0.85

Apparent power = 0.75

Frequency = 60 Hz

Suppose we need to calculate the impedance Z₁

The impedance Z₁ dissipates 10 kW with a power factor of 0.85 lagging

`\cos\theta=0.85`

`\theta=\cos^(-1)(0.85)`

`\theta=31.78^(\circ)`

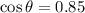
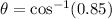
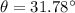
We need to calculate the impedance Z₁

Using formula of the impedance Z₁

`z_(1)=P_(1)+jQ_(1)`

`z_(1)=P_(1)+j(10)/(0.85)\sin\theta`

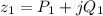
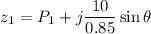
Put the value into the formula

`z_(1)=10+j(10)/(0.85)\sin31.78`

`z_(1)=10+j6.19\ kVA`

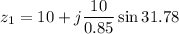
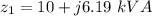
Hence, The impedance Z₁ is
`10+j6.19\ kVA`