Answer: 95% confidence interval would be (0.555,0.745).
Explanation:
Since we have given that
n = 97
x = 63
So, we get that
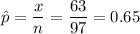
At 95% confidence interval , z = 1.96
so, Margin of error would be

So, interval would be

Hence, 95% confidence interval would be (0.555,0.745).