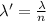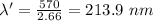Question

In a physics lab, light with a wavelength of 570 travels in air from a laser to a photocell in a time of 16.5 . When a slab of glass with a thickness of 0.865 is placed in the light beam, with the beam incident along the normal to the parallel faces of the slab, it takes the light a time of 21.3 to travel from the laser to the photocell. What is the wavelength of the light in the glass? Use 3.00×10^8 m/s for the speed of light in a vacuum.

Answer 1

Wavelength is calculated as 213.9 nm

Solution:

As per the question:

Wavelength of light = 570 nm

Time, t = 16.5 ns

Thickness of glass slab, d = 0.865 ns

Time taken to travel from laser to the photocell, t' = 21.3

Speed of light in vacuum, c =
`3* 10^(8)\ m/s`

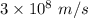
Now,

To calculate the wavelength of light inside the glass:

After the insertion of the glass slab into the beam, the extra time taken by light to cover a thickness t = 0.865 m is:

t' - t = 21.3 - 16.5 = 4.8 ns

Thus

`(d)/((c)/(n)) - (d)/(v) = 4.8* 10^(- 9)`

`(0.8656)/((c)/(n)) - (0.865)/(v) = 4.8* 10^(- 9)`

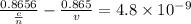
where

n = refractive index of the medium

v = speed of light in medium

`(0.8656)/((c)/(n)) - (0.865)/(v) = 4.8* 10^(- 9)`

`n = (4.8* 10^(- 9)* 3.00* 10^(8))/(0.865) + 1`

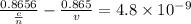
n = 2.66

Now,

The wavelength in the glass:

`\lambda' = (\lambda )/(n)`

`\lambda' = (570)/(2.66) = 213.9\ nm`