Question

Some types of algae have the potential to cause damage to river ecosystems. Suppose the accompanying data on algae colony density (y) and rock surface area (x) for nine rivers is a subset of data that appeared in a scatterplot in a research paper in a scientific journal.

x 50 55 50 79 44 37 70 45 49
y 152 48 22 35 43 171 13 185 25
(a) Compute the equation of the least-squares regression line. (Round your numerical values to five decimal places.)

Answer 1

The equation of the regression line is:

`y~=~234.56158 ~-~ 2.95835 \cdot x`

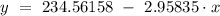
Explanation:

The Least Squares Regression Line is the line that makes the vertical distance from the data points to the regression line as small as possible. It’s called a “least squares” because the best line of fit is one that minimizes the variance.

We have the following data:

`\begin{array}cX&50&55&50&79&44&37&70&45&49\\Y&152&48&22&35&43&171&13&185&25\end{array}`

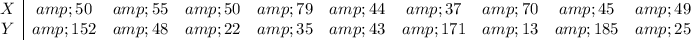
To find the line of best fit for the points:

Step 1: Find
`X\cdot X` and
`X\cdot Y` as it was done in the table

Step 2: Find the sum of every column:

`\sum{X} = 479 ~,~ \sum{Y} = 694 ~,~ \sum{X \cdot Y} = 32784 ~,~ \sum{X^2} = 26897`

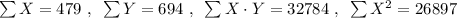
Step 3: Use the following equations to find a and b:

`\begin{aligned}        a &= \frac{\sum{Y} \cdot \sum{X^2} - \sum{X} \cdot \sum{XY} }{n \cdot \sum{X^2} - \left(\sum{X}\right)^2} =             ( 694 \cdot 26897 - 479 \cdot 32784)/( 9 \cdot 26897 - 479^2) \approx 234.56158 \\ \\b &= \frac{ n \cdot \sum{XY} - \sum{X} \cdot \sum{Y}}{n \cdot \sum{X^2} - \left(\sum{X}\right)^2}        = ( 9 \cdot 32784 - 479 \cdot 694 )/( 9 \cdot 26897 - \left( 479 \right)^2) \approx -2.95835\end{aligned}`

Step 4: Assemble the equation of a line

`\begin{aligned} y~&=~a ~+~ b \cdot x \\y~=~234.56158 ~-~ 2.95835\cdot x\end{aligned}`

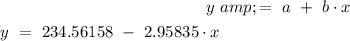
The graph of the regression line is: