Question

An astronaut goes out for a "space-walk" at a distance above the earth equal to the radius of earth. What is her acceleration due to gravity at that point?

a) zero
b) g
c) g /2
d) g/4
e) g/2

Answer 1

d)
`(g)/(4)`

Step-by-step explanation:

The acceleration due to gravity on the surface of the Earth is given as:

`g=(GM)/(R^2)`

Where, 'G' is universal gravitational constant, 'M' is the mass of Earth, and 'R' is the radius of Earth.

Now, when the astronaut goes above the Earth equal to the radius of Earth, the distance between the center of Earth and the astronaut is twice the radius.

Therefore, new distance between the astronaut and Earth's center is '2R'.

Now, the acceleration due to gravity at point is given as:

`g_(new)=(GM)/((2R)^2)\\g_(new)=(GM)/(4R^2)\\g_(new)=(1)/(4)((GM)/(R^2))\\\\But,(GM)/(R^2)=g.\ So,\\g_(new)=(1)/(4)g=(g)/(4)`

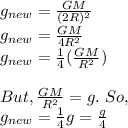
Hence, her acceleration due to gravity at that point is
`(g)/(4)`