Answer: The required matrix A is
![A=\left[\begin{array}{ccc}0&0&0\\0&0&0\\4&0&0\\0&4&0\\0&0&4\end{array}\right]_(5*3) .](https://img.qammunity.org/2020/formulas/mathematics/college/lzzfwd5fmhzt8s6cw41rz48h2ve54oopvh.png)
Step-by-step explanation: We are given the following linear transformation :

We are to find the matrix A relative to the bases
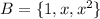 and
and
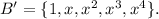
We have
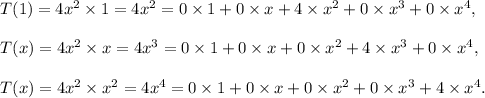
Therefore, the matrix A is of order 5 × 3, given by
![A=\left[\begin{array}{ccc}0&0&0\\0&0&0\\4&0&0\\0&4&0\\0&0&4\end{array}\right]_(5*3) .](https://img.qammunity.org/2020/formulas/mathematics/college/lzzfwd5fmhzt8s6cw41rz48h2ve54oopvh.png)
Thus, the required matrix A is
![A=\left[\begin{array}{ccc}0&0&0\\0&0&0\\4&0&0\\0&4&0\\0&0&4\end{array}\right]_(5*3) .](https://img.qammunity.org/2020/formulas/mathematics/college/lzzfwd5fmhzt8s6cw41rz48h2ve54oopvh.png)