Question

The wavelength of light emitted by a particular laser is 477 nm. This laser light illuminates two slits that are 54.0 µm apart, and a screen is 1.40 m from the slits. What is the angular separation between the n = 2 and n = ?2 maxima?

Answer 1

The angular separation is 2.024°.

Step-by-step explanation:

Given that,

Wavelength = 477 nm

Distance of two slits d= 54.0 μm

Distance from screen = 1.40 m

We need to calculate the angular separation

Using formula of angular separation

`\sin\theta= n\lambda`

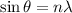
Where, d = distance

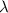`\lambda` = wavelength

Put the value into the formula

`\sin\theta=(n\lambda)/(2d)`

`\theta=\sin^(-1)((2*477*10^(-9))/(54.0*10^(-6)))`

`\theta=1.012^(\circ)`

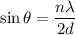
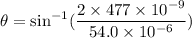
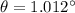
The angular separation is

`angular\ separation =2\theta`

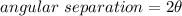
Put the value into the formula

`angular\ separation =2*1.012`

`angular\ separation =2.024^(\circ)`

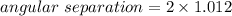
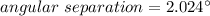
Hence, The angular separation is 2.024°.