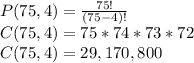Question

Seventy-five people buy a raffle ticket for a cake drawing with four cakes. If four tickets are to be drawn, how many ways are there to award the cakes if the four cakes are a. identical? b. different?

Answer 1

a. 1,215,454 ways

b. 29,170,800 ways

Explanation:

a. If the four cakes are identical, order does not matter, and the total number of ways to award the cakes is given by a combination, C(75,4):

`C(75,4) = (75!)/((75-4)!4!)\\C(75,4) = (75*74*73*72)/(4*3*2*1)\\C(75,4) = 1,215,454`

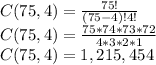
b. If the four cakes are different, order does matter, and the total number of ways to award the cakes is given by a permutation, P(75,4):

`P(75,4) = (75!)/((75-4)!)\\C(75,4) = 75*74*73*72\\C(75,4) = 29,170,800`