Answer:
Explanation:
Given that costs are rising for all kinds of medical care. The mean monthly rent at assisted-living facilities was reported to have increased 17% over the last five years to $3486
Sample size n =120
Population std dev =
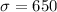
Since sigma is known we can use Z critical values for confidence interval
a) 90% confidence interval estimate of the population mean monthly rent
=Mean±1.645*std error
=

b) 95% confidence interval estimate of the population mean monthly rent.
==Mean±1.96*std error
=
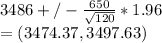
c) 99% confidence interval estimate of the population mean monthly rent.
=Mean±2.58*std error
=
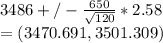
d) Width increases as confidence level increases. This is reasonable because margin of error increases due to increase in critical value.