Question

Population Growth. Port St. Lucie, Florida, had the United States fastest growth rate among cities with a population of 100,000 or more between 2003 and 2004. In 2003, the population was 103, 800 and increasing at a rate of 12% per year. In what year should the population reach 209,000 ? (Let t = 0 correspond to 2003.) Apply the formula N = N0 e^rt, where N represents the number of people. Round your answer to one desimal place. T = ______________years.The tolerance is ±2%

Answer 1

In 2009

Explanation:

Since, the formula of population after t years,

`N=N_0 e^(rt)`

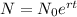
Where,

r = rate of growing per year,

Here, r = 12% = 0.12,

So, the population formula would be,

`N=N_0 e^(0.12t)`

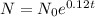
If the population is estimated since 2003,

i.e. for 2003, t = 0,

We have N = 103, 800 for 2003,

`\implies 103800 = N_0 e^(0.12* 0)=N_0 e^0 = N_0`

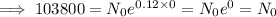
Thus, the function that shows the population after t years,

`N = 103800 e^(0.12t)`

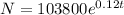
If N = 209,000,

`209000 = 103800 e^(0.12t)`

`(209000)/(103800) = e^(0.12t)`

`2.01349 = e^(0.12t)`

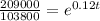
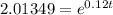
Taking ln on both sides,

`\ln ( 2.01348 ) = 0.12t`

`\implies t = (\ln(2.01348))/(0.12)=5.8\approx 6`

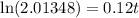
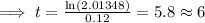
∵ 2003 + 6 = 2009

Hence, in 2009, the population should reach 209,000.