Question

Starting from zero, the electric current takes 2 seconds to reach half its maximum possible value in an RL circuit with a resistance R, an inductance L and a battery of emf E. How long will the current take to reach 75% its maximum value (measured from the moment when I = 0)?a. 10 s

b. 8 s
c. 4 s
d. 2 s
e. 1 s

Answer 1

time=4s

Step-by-step explanation:

we know that in a RL circuit with a resistance R, an inductance L and a battery of emf E, the current (i) will vary in following fashion

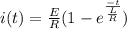`i(t)=(E)/(R)(1-e^(-t)/((L)/(R)))`, where
`i`max=
`(E)/(R)`

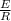
Given that, at i(2)=
`(imax)/(2) =(E)/(2R)`

⇒
`(E)/(2R)=(E)/(R)(1-e^(-2)/((L)/(R)))`

⇒
`(1)/(2)=1-e^(-2)/((L)/(R))`

⇒
`(1)/(2)=e^(-2)/((L)/(R))`

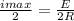
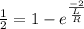
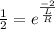
Applying logarithm on both sides,

⇒
`log((1)/(2))=(-2)/((L)/(R))`

⇒
`log(2)=(2)/((L)/(R))`

⇒
`(L)/(R)=(2)/(log2)`

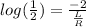
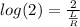
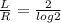
Now substitute
`i(t)=(3)/(4)imax=(3E)/(4R)`

⇒
`(3E)/(4R)=(E)/(R)(1-e^(-t)/((L)/(R)))`

⇒
`(3)/(4)=1-e^(-t)/((L)/(R))`

⇒
`(1)/(4)=e^(-t)/((L)/(R))`

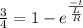
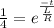
Applying logarithm on both sides,

⇒
`log((1)/(4))=(-t)/((L)/(R))`

⇒
`log(4)=(t)/((L)/(R))`

⇒
`t=log4(L)/(R)`

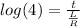
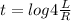
now subs.
`(L)/(R)=(2)/(log2)`

⇒
`t=log4(2)/(log2)`

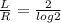
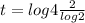
also
`log4=log2^(2)=2log2`

⇒
`t=2log2(2)/(log2)`

⇒
`t=4`