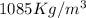Question

A cube of volume 5.50×10−3m3 and density 7.50×103kg/m3 hangs from a cable. When the cube has the lower half of its volume submerged in an unknown liquid, the tension in the cable is 375 N. What is the density of the liquid? (Ignore the small buoyant force exerted by the air on the upper half of the cube.)

Answer 1

To solve this problem it is necessary to apply the concepts related to the balance of Forces, as well as Newton's second Law and the relationship between density, volume and mass.

Newton's second law indicates that

`F = ma \rightarrow m=mass, a = acceleration`

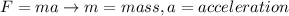
At the same time we have that the density is equal to

\rho = \frac{m}{V} \rightarrow m = mass, V=Volume

In other words, Newton's second law could also be expressed as

`F = m \rho V`

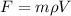
For this problem we will have the forces expressed with two types of densities. The force caused by the weight will have the density of the respective material while the support force will allow us to know the density of the liquid.

From the balance of the bodies we know that the weight of the cube is equal to the tension exerted and the bearing force, therefore,

Weight of cube = Tension + Buoyant force

`F_w =  F_l+T`

`\rho_1 V g = \rho ((V)/(2))g + T`

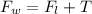
Replacing

`(7.5 *10^3)(5.5 *10^(-3))(9.8) = \rho((5.5 *10^(-3))/(2))(9.8) + 375`

`\rho = 1085 Kg/m^3`

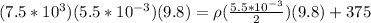
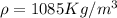
Therefore the density of the liquid is
`1085 Kg/m^3`