Question

You have four sweaters, five pairs of pants, and three pairs of shoes. How many different combinations can you make, wearing

one of each? Explain your answer.
a. 4.5+3 = 23
b. 4.5 = 20
C. 4.5.3 = 60
4+ 5+ 3 = 12​

Answer 1

c

Explanation:

big brain

Answer 2

C.
`4\cdot 5\cdot 3 = 60`

Explanation:

Given:

Number of sweaters are,
`S=4`

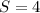
Number of pair of pants are,
`P=5`

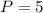
Number of pairs of shoes are,
`H=3`

Now, as per question, we have to choose one from each type.

Now, number of ways of choosing one sweater from 4 sweaters is
`n(S)= 4\ ways`.

Number of ways of choosing one pair of pants from 5 pair of pants is
`n(P)= 5\ ways`.

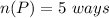Number of ways of choosing one pair of shoes from 3 pairs of shoes is
`n(H)= 3\ ways`.

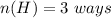Therefore, choosing one from each type is the intersection of all. So,

`n(S\cap P\cap H)=n(S)\cdot n(P)\cdot n(H)\\n(S\cap P\cap H)=4\cdot 5\cdot 3\\n(S\cap P\cap H)=60`

Therefore, 60 different combinations can be made wearing one of each type.