Question

You kick a soccer ball with a speed of 18 m/s at an angle of 43. How long does it take the the ball to reach the top of its trajectory

Answer 1

1.25 s

Step-by-step explanation:

The motion of the soccer ball is an example of a projectile motion.

So, time taken by the ball to reach the top of the trajectory is exactly half of the total time of flight of the soccer ball.

In a projectile motion, the projectile is thrown at an angle to the ground with some initial velocity. The motion can be divided into two independent direction motions; one in the horizontal direction and the other in the vertical direction.

The time of flight is the time taken by the projectile to reach the ground again.

The formula for time of flight is given as:

`T=(2u\sin \theta)/(g)\\Where,T\to \textrm{Time of flight}\\u\to \textrm{Initial velocity of ball}\\\theta \to \textrm{Angle of projection}\\g\to \textrm{Acceleration due to gravity}`

Here,
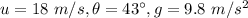`u=18\ m/s,\theta=43\°,g=9.8\ m/s^2`. Therefore,

`T=(2* 18* \sin 43\°)/(9.8)=2.505\ s`

Now, the time taken to reach the top is half of the total time. Therefore,

`T_(top)=(T)/(2)=(2.505)/(2)=1.25\ s`

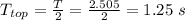
Therefore, it takes 1.25 s for the ball to reach the top of its trajectory.