Answer:
Angle of first order maximum,
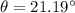
Step-by-step explanation:
Given that,
Wavelength of the light,
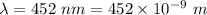
Number of lines, N = 8000 per cm
The relation between the number of lines and the slit width is given by :
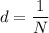
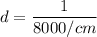
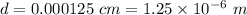
The equation of grating is given by :
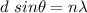
n = 1
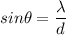
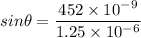
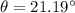
So, the angle of the first-order maximum is 21.19 degrees. Hence, this is the required solution.