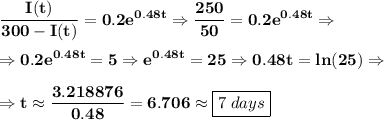Question

The flu is spreading throughout a UT residence hall of 300 students. It is highly contagious and long in duration, and no effective antiviral nor vaccine is yet available due to the extreme degree of mutation found in this particular strain of virus. No student is able to recover and all sick students are contagious. It is reasonable to assume that the rate at which students are getting ill is proportional to the product of the number of sick students and the number of healthy ones because there must be an interaction between a healthy and sick student to pass along the disease. At the time when there were already a total of 30 sick students, it was observed that about 13 more students per day were falling ill. Currently there are a total of 50 sick students. Now, in how many days will a total of 250 students in the residence hall get infected? (Use a constant of propottionality accurate up to four decimal places.)

Answer 1

7 days

Explanation:

Let I(t) be the number of ill students at day t.

Since the rate at which students are getting ill is proportional to the product of the number of sick students and the number of healthy ones

I'(t) = k*I(t)(300-I(t)) for some constant k.

We have that at the time t1 when there were already a total of 30 sick students, it was observed that about 13 more students per day were falling ill, so

13 = I'(t1) = k*30(300-30) ===> 8100*k=13 ===> k=0.0016

and

I'(t) = 0.0016*I(t)(300 - I(t))

This is an ordinary differential equation of 1st order which can be solved by separation of variables

`\bf \displaystyle(dI)/(dt)=0.0016*I(300 - I)\Rightarrow \displaystyle(dI)/(I*(300 - I))=0.0016dt`

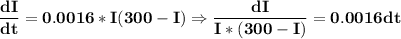
the term

`\bf \displaystyle(dI)/(I(t)(300 - I(t)))`

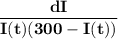
can be broken down into partial fractions as

`\bf \displaystyle(dI)/(I(300 - I))=\displaystyle(dI/300)/(I)+\displaystyle(dI/300)/(300-I)=\displaystyle(1)/(300)\displaystyle(dI)/(I)+\displaystyle(1)/(300)\displaystyle(dI)/((300-I))`

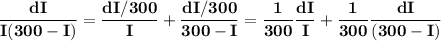
and our differential equation becomes

`\bf \displaystyle(1)/(300)\displaystyle(dI)/(I)+\displaystyle(1)/(300)\displaystyle(dI)/((300-I))=0.0016dt\Rightarrow \displaystyle(dI)/(I)+\displaystyle(dI)/((300-I))=0.48dt`

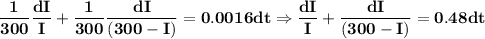
Integrating both sides

`\bf \displaystyle\int\displaystyle(dI)/(I)+\displaystyle\int\displaystyle(dI)/((300-I))=\displaystyle\int0.48dt\Rightarrow ln(I)-ln(300-I)=0.48t +C\Rightarrow\\\\\Rightarrow ln\left(\displaystyle(I)/(300-I)\right)=0.48t+C\Rightarrow \displaystyle(I(t))/(300-I(t))=C_1e^(0.48t)`

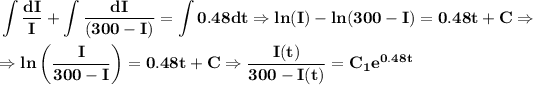
Currently there are a total of 50 sick students, so I(0) = 50 and

`\bf \displaystyle(I(0))/(300-I(0))=C_1e^(0.48*0)\Rightarrow C_1=\displaystyle(50)/(300-50)\Rightarrow C_1=0.2`

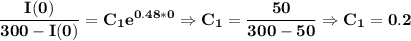
hence

`\bf \displaystyle(I(t))/(300-I(t))=0.2e^(0.48t)\Rightarrow I(t)=0.2e^(0.48t)(300-I(t))\Rightarrow\\\\\Rightarrow I(t)=60e^(0.48t)-0.2e^(0.48t)I(t)\Rightarrow I(t)+0.2e^(0.48t)I(t)=60e^(0.48t)\Rightarrow\\\\\Rightarrow (1+0.2e^(0.48t))I(t)=60e^(0.48t)\Rightarrow \boxed{I(t)=\displaystyle(60e^(0.48t))/(1+0.2e^(0.48t))}`

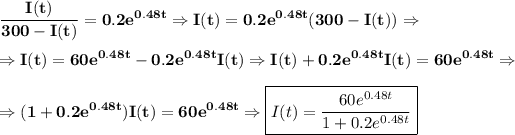
in how many days will a total of 250 students in the residence hall get infected?

We must find a value of t such that I(t) = 250

`\bf \displaystyle(I(t))/(300-I(t))=0.2e^(0.48t)\Rightarrow \displaystyle(250)/(50)=0.2e^(0.48t)\Rightarrow\\\\\Rightarrow 0.2e^(0.48t)=5\Rightarrow e^(0.48t)=25\Rightarrow 0.48t=ln(25)\Rightarrow\\\\\Rightarrow t \approx \displaystyle(3.218876)/(0.48)=6.706\approx\boxed{7 \;days}`