Answer: The molar heat of vaporization is 30.6 kJ/mol
Step-by-step explanation:
To calculate the molar heat of vaporization, we use the equation given by Clausius-Clapeyron, which is:

Where,
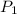 = vapor pressure at temperature
= vapor pressure at temperature
 = 134 mmHg
= 134 mmHg
 = vapor pressure at temperature
= vapor pressure at temperature
 (atmospheric pressure) = 760 mmHg
(atmospheric pressure) = 760 mmHg
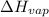 = molar heat of vaporization
= molar heat of vaporization
R = gas constant = 8.314 J/mol.K
 = temperature of dichloromethane =
= temperature of dichloromethane =
![0^oC=[273+0]K=273K](https://img.qammunity.org/2020/formulas/chemistry/college/733w04z6czr6xgjrsz9xmhth5059wvldjv.png)
 = normal boiling point of dichloromethane =
= normal boiling point of dichloromethane =
![40^oC=[273+40]K=313K](https://img.qammunity.org/2020/formulas/chemistry/college/xa2vdau617zxwy8ync1scl0ixz0pjr72hw.png)
Putting values in above equation, we get:
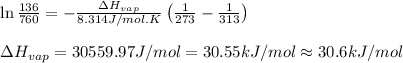
Hence, the molar heat of vaporization is 30.6 kJ/mol