Question

To assess the accuracy of a kitchen scale a standard weight known to weigh 1 gram is weighed a total of n times and the mean, , of the weighings is computed.

Suppose the scale readings are Normally distributed with unknown mean, µ, and standard deviation = 0.01 g.

How large should n be so that a 90% confidence interval for µ has a margin of error of ± 0.0001?

Answer 1

Answer: 27061

Explanation:

Given : The scale readings are Normally distributed with unknown mean, µ, and standard deviation
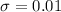`\sigma= 0.01` g.

Confidence interval = 90%

We know that the critical value for 90% confidence interval = z*=1.645 (by z-table)

Margin of error E= ± 0.0001

Now, Required minimum size : n=
`((z^*\cdot\sigma)/(E))^2`

`=((1.645\cdot0.01)/(0.0001))^2`

`=((0.01645)/(0.0001))^2`

`=(164.5)^2=27060.25\approx27061`

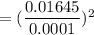
Hence, n= 27061.