Question

The profit that the vendor makes per day by selling x pretzels is given by the function P(x) = -0.004 x^2 + 2.8x - 350. Find the number of pretzels that must be sold to maximize profit A) 325 pretzels B) 340 pretzels C) 350 pretzels

Answer 1

To find the number of pretzels that must be sold to maximize profit, we can use the vertex formula to calculate the value of x. Plugging the given values into the formula, we find that the number of pretzels that must be sold is 350 pretzels.

Step-by-step explanation:

To find the number of pretzels that must be sold to maximize profit, we need to find the maximum value of the profit function. The profit function is given by P(x) = -0.004x^2 + 2.8x - 350.

To find the number of pretzels that maximizes profit, we can use the vertex formula x = -b/(2a).

For the given function, a = -0.004, b = 2.8, and c = -350. Plugging these values into the formula, we get x = -2.8/(2*(-0.004)) = 350.

Therefore, the number of pretzels that must be sold to maximize profit is 350 pretzels.

Answer 2

Answer: Option 'c' is correct.

Step-by-step explanation:

Since we have given that

`P(x)=-0.004x^2+2.8x-350`

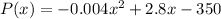
So, we will first derivative it w.r.t to x, we get that

`P'(x)=-0.008x+2.8`

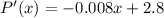
For critical points, we get that

`P'(x)=0\\\\-0.008x+2.8=0\\\\-0.008x=-2.8\\\\x=(2.8)/(0.008)\\\\x=350`

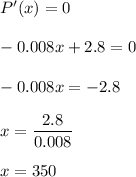
Now, we will check for maximum profit.

So, we will find Second derivation and then put the value of x = 350 in it.

`p''(x)=-0.008<0`

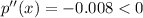
So, it will give maximum profit.

Hence, At 350 pretzels, there must be maximum profit.

Therefore, Option 'c' is correct.