Answer:
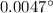
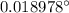
B) Dim
Step-by-step explanation:
 = Angle
= Angle
a = Pupil diameter
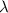 = Wavelength = 543 nm
= Wavelength = 543 nm
Angular resolution is given by
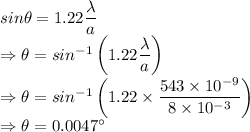
For the dim light the angle is
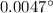
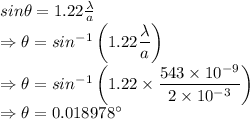
For the bright light the angle is
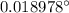
The angular separation and sharpness are inversely related. Here, the dim light will produce a sharp image.
Hence, option B is correct