Question

When a sinusoidal wave with speed 20 m/s , wavelength 35 cm and amplitude of 1.0 cm passes, what is the maximum speed of a point on the string?

Answer 1

To solve this problem it is necessary to apply the concepts related to frequency as a function of speed and wavelength as well as the kinematic equations of simple harmonic motion

From the definition we know that the frequency can be expressed as

`f = (v)/(\lambda)`

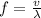
Where,

`v = Velocity \rightarrow 20m/s`

`\lambda = Wavelength \rightarrow 35*10^(-2)m`

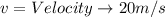
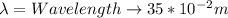
Therefore the frequency would be given as

`f = (20)/(35*10^(-2))`

`f = 57.14Hz`

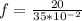
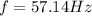
The frequency is directly proportional to the angular velocity therefore

`\omega = 2\pi f`

`\omega = 2\pi *57.14`

`\omega = 359.03rad/s`

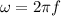
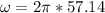
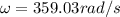
Now the maximum speed from the simple harmonic movement is given by

`V_(max) = A\omega`

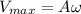
Where

A = Amplitude

Then replacing,

`V_(max) = (1*10^(-2))(359.03)`

`V_(max) = 3.59m/s`

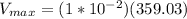
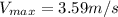
Therefore the maximum speed of a point on the string is 3.59m/s