Question

2 intersecting lines are shown. A line with points T, R, W intersects a line with points S, R, V at point R. 4 angles are created. Clockwise, from the top, the angles are blank, (3 x) degrees, blank, (x + 40) degrees.

What is the value of x?

20
35
60
70

Answer 1

20

Explanation:

Answer 2

The figure is attached below.

The value of x = 20.

Explanation:

Given:

See the Diagram below

T-R-W is the Line and

S-R-V is the Line intersecting each other at point R making angles in clockwise as below

m∠ SRW = blank

m∠ WRV = 3x

m∠ VRT = blank

m∠ TRS = ( x + 40 )

To Find:

x = ?

Solution:

Vertical Opposite Angles Theorem:

Vertically Opposite Angles are the angles opposite each other when two lines cross and are always EQUAL.

Here in the figure

m∠ WRV and m∠ TRS are Vertically Opposite Angles

∴ m∠ WRV = m∠ TRS

∴ 3x = (x +40)

∴ 3x -x = 40

∴ 2x = 40

∴
`x=(40)/(2) \\\\\therefore x = 20`

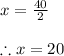
The value of x = 20.