Question

Two strings are adjusted to vibrate at exactly 202 Hz. Then the tension in one string isincreased slightly. Afterward, three beats per second are heardwhen the strings vibrate at the same time. What is the newfrequency of the string that was tightened?

Answer 1

The concepts necessary to solve this problem are framed in the expression of string vibration frequency as well as the expression of the number of beats per second conditioned at two frequencies.

Mathematically, the frequency of the vibration of a string can be expressed as

`f = (1)/(2L)\sqrt{(T)/(\mu)}`

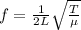
Where,

L = Vibrating length string

T = Tension in the string

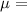`\mu =` Linear mass density

At the same time we have the expression for the number of beats described as

`n = |f_1-f_2|`

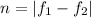
Where

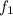`f_1` = First frequency

`f_2` = Second frequency

From the previously given data we can directly observe that the frequency is directly proportional to the root of the mechanical Tension:

`f \propto √(T)`

If we analyze carefully we can realize that when there is an increase in the frequency ratio on the tight string it increases. Therefore, the beats will be constituted under two waves; one from the first string and the second as a residue of the tight wave, as well

`n = f_2-f_1`

`f_2 = n+f_1`

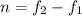
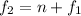
Replacing
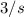`3/s`for n and 202Hz for
`f_1,`

`f_2 = 3/s + 202Hz`

`f_2 = 3/s((1Hz)/(1/s))+202Hz`

`f_2 = 206Hz`

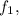
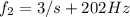
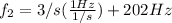
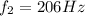
The frequency of the tightened is 205Hz