To solve this problem we must basically resort to the kinematic equations of movement. For which speed is defined as the distance traveled in a given time. Mathematically this can be expressed as
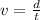
Where
d = Distance
t = time
For which clearing the time we will have the expression
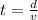
Since we have two 'fluids' in which the sound travels at different speeds we will have that for the rock the time elapsed to feel the explosion will be:
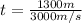

In the case of the atmosphere -composite of air- the average speed of sound is 343m / s, therefore it will take
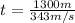
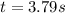
The total difference between the two times would be
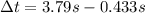
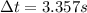
Therefore 3.357s will pass between when they feel the explosion and when they hear it