Question

When trying to hire managers and executives, companies sometimes verify the academic credentials described by the applicants. One company that performs these checks summarized their findings for a six-month period. Of the 91 applicants whose credentials were checked, 16 lied about having a degree.(a) Find the proportion of applicants who lied about having a degree, and find the standard error.(b) Consider these data to be a random sample of credentials from a large collection of similar applicants. Give a 90%confidence interval for the true proportion of applicants who lie about having a degree.

Answer 1

a) p ≅ 0.18

√V(X) ≅ 3.66

b) [0.1139; 0.2460]

Explanation:

Hello!

The variable of interest is the number of applicants that lied about having a degree. This variable is discrete and has two posible outcomes, that the applicant lied about having a degree (this will be or "success") and that the aplicant didn't lie about having a degree (in this case this answe is counted as "failure" since the proportion of interest is the number of aplicants that lied)

a)

To calculate the proportion you have to divide the number of "success" by the total of the sample, in this case:

`p= (x)/(n) = (16)/(91) = 0.1758 ≅ 0.18`

Considering the study variable to have binomial distribution the variance is calculated as:

`V(X)= n*p*(1 - p) = 91 * 0.18 * 0.82= 13.4316`

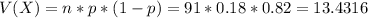
Then you apply the square root to the calculated variance to calculate the standard error:

`√(V(X)) = √(13.4316) = 3.66`

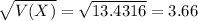
b)

To calculate the confidence interval, you have to apply the Central Limit Theorem and approximate the distribution of the sample proportion to normal, symbolically ^p ≈ N(p; (p(1-p))/n)

Then the formula for the interval is:

^p ±
`Z_(1-\alpha /2)`*
`\sqrt{(p(1-p))/(n) }`

`Z_(1-\alpha /2) = Z_(0.95) = 1.64`

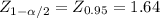
0.18 ± 1.64*
`\sqrt{(0.18(1-0.18))/(91) }`

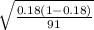
[0.1139; 0.2460]

I hope you have a SUPER day!