Answer:
c(t) =
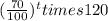
Explanation:
The concentration of the medicine reduce 30% for each passing hour.
After one hour, it will reduce 30% of its concentration, that is remaining concentration of the medicine is (100 - 30)% = 70%
After 1 hour, the concentration will be,
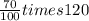 milligrams per liter.
milligrams per liter.
After 2 hour, the quantity will be
 =
=
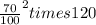 .
.
Hence, after t hours the concentration of the medicine can be represented as, c(t) =
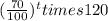 .
.