Answer:
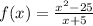
Explanation:
Given:
We need to check the continuity of the functions at
 .
.
Option 1:
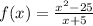
Plug in 5 for 'x' and check the value of
 .
.
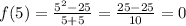
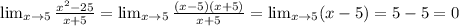
So, the function is defined at and around
 and equal to 0. So, it is continuous at
and equal to 0. So, it is continuous at
 .
.
Option 2:
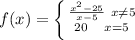
The given function is defined at
 and is equal to 20 but it has a different value around 5.
and is equal to 20 but it has a different value around 5.
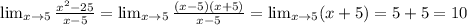
So, the function has a value of 10 around
 and equal to 20 at
and equal to 20 at
 . So, it is not continuous at
. So, it is not continuous at
 .
.
Option 3:
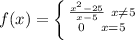
The given function is defined at
 and is equal to 0 but it has a different value around 5.
and is equal to 0 but it has a different value around 5.
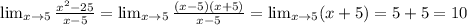
So, the function has a value of 10 around
 and equal to 0 at
and equal to 0 at
 . So, it is not continuous at
. So, it is not continuous at
 .
.