Question

Find the equation of the axis of symmetry and the coordinates of

function y = -2x + 6x - 1.
*= 3; vertex: (3, 35)
* = -1.5; vertex: (-1.5, -5.5)
x= -1.5; vertex (-1.5, -14.5)
x = 1.5; vertex (1.5, 3.5)​

Answer 1

Axis of symmetry:
`x=1.5`

Vertex is at (1.5, 3.5).

Explanation:

Given:

The equation of the parabola is given as:

`y=-2x^2+6x-1`

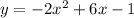
The standard form of a parabola is given as:

`y=ax^2+bx+c`

On comparing the given equation with the standard form, we get:

`a=-2,b=6,\ and\ c=-1`

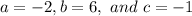
We know that, for a parabola, the axis of symmetry is given as:

`x=-(b)/(2a)\\x=-(6)/(2(-2))\\x=-(6)/(-4)=(3)/(2)\\x=1.5`

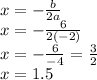
Therefore, the equation of the axis of symmetry is
`x=1.5`

The vertex of a parabola is given as
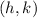`(h,k)` where:

`h=-(b)/(2a)\\h=-(6)/(-4)=1.5\\\\k=f(h)=f(1.5)\\k=-2(1.5)^2+6(1.5)-1\\k=-2(2.25)+9-1\\k=-4.5+8=3.5`

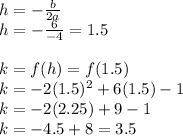
Therefore, the vertex of the given parabola is at the point (1.5, 3.5)