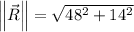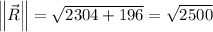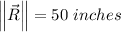Question

Two vectors, X and Y, form a right angle. Vector X is 48 inches long and vector Y is 14 inches long. The length of the

resultant vector is
inches

Answer 1

50 inches

Step-by-step explanation:

edge 2o2o

Answer 2

`\left \| \vec R \right \|=50\ inches`

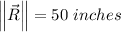
Step-by-step explanation:

Vectors In The Plane

Given two vectors
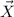`\vec X` and
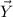`\vec Y`, their sum is shown as the vector
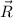`\vec R` in the image below. It can be seen the magnitude of R is the hypotenuse of a right triangle. i.e.

`\left \| \vec R \right \|=√(\left \| X \right \|^2+\left \| Y \right \|^2)`

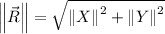
The magnitude of
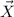`\vec X` is 48 inches and the magnitude of
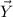`\vec Y` is 14 inches, the magnitude of R is

`\left \| \vec R \right \|=√(48^2+14^2)`

`\left \| \vec R \right \|=√(2304+196)=√(2500)`

`\left \| \vec R \right \|=50\ inches`