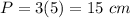Question

Given ΔABC, AB = BC = AC . Area of ΔABC = 25 sqrt 3/4 cm. Find the perimeter of ΔABC.

Answer 1

The perimeter of triangle ABC is 15 cm

Explanation:

we know that

An equilateral triangle has three equal sides and and three equal interior angles (each angle measure 60 degrees)

In this problem

Triangle ABC is an equilateral triangle

Because

AB=BC=AC

The area of a equilateral triangle (applying the law of sines) is equal to

`A=(1)/(2)b^(2)sin(60^o)`

where

b is the length side of the equilateral triangle

we have that

`A=(25√(3))/(4)\ cm^2`

`sin(60^o)=(√(3))/(2)`

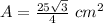
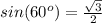
substitute

`(25√(3))/(4)=(1)/(2)b^(2)((√(3))/(2))`

`(25√(3))/(4)=b^(2)((√(3))/(4))`

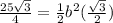
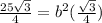
simplify

`b^(2)=25`

`b=5\ cm`

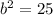
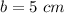
Find the perimeter of triangle ABC

The perimeter is equal to

`P=3b`

substitute the value of b

`P=3(5)=15\ cm`