Question

Find all the zeros of the function. Y=x^4 -6x^2 +8

Answer 1

+/- 2, +/-
`√(2)`

Explanation:

Answer 2

The zeroes of the given equation are x = √2 , -√2 , 2 , -2.

Explanation:

The given quadratic equation is y =
`x^(4)- 6x^(2)+8`

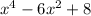
To find the zeroes , put y = 0.

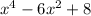`x^(4)- 6x^(2)+8` = 0

Put
`x^(2)`=t

The new equation is
`t^(2) -6t +8=0`

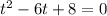
On factorising ,

`(t - 4)*(t - 2)=0`

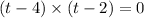
Hence t = 2 or t = 4

On resubstituting the value of t in terms of x ,

`x^(2)` = 2 or
`x^(2)` = 4

Taking square root of above equation , we get

x = √2,-√2,2,-2

These are the 4 roots of the given equation .