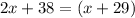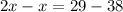Question

I need help with geometry.
Find x.

Answer 1

Part 9)
`x=5`

Part 10)
`x=-9`

Explanation:

we know that

The Midpoint Theorem states that: The segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side

Part 9) we know that

Point Q is the midpoint segment XY (QY=QX)

Point R is the midpoint segment XW (RW=RX)

Applying the Midpoint Theorem

RQ is parallel to WY

and

`RQ=(1)/(2)WY`

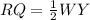
we have

`RQ=2x-3\\WY=x+9`

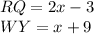
substitute

`2x-3=(1)/(2)(x+9)`

solve for x

`4x-6=(x+9)`

`4x-x=9+6`

`3x=15`

`x=5`

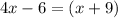
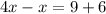
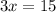
Part 10) we know that

Point B is the midpoint segment TS (BS=BT)

Point C is the midpoint segment RS (CS=CR)

Applying the Midpoint Theorem

BC is parallel to TR

and

`BC=(1)/(2)TR`

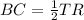
we have

`BC=x+19\\TR=x+29`

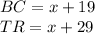
substitute

`x+19=(1)/(2)(x+29)`

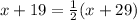
solve for x

`2x+38=(x+29)`

`2x-x=29-38`

`x=-9`