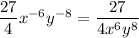Answer:
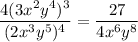
Explanation:
Given:
The expression to simplify is given as:
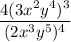
First, we will simplify the numerator and denominator separately using the law of indices:
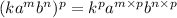
The numerator is simplified as:
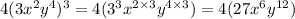
The denominator is simplified as:
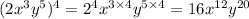
Now, we divide the simplified numerator by the simplified denominator. This gives,
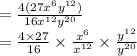
Now, we simplify using another law of indices which is given as:
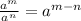
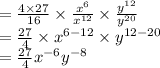
Now, we write the answer using only positive exponents and thus we use the given law of indices:
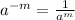
Therefore, the simplified form is: