Question

Kevin works at an electronics store as a salesperson. Kevin earns a 4% commission on the total dollar amount of all phone sales he makes, and earns a 5% commission on all computer sales. Kevin had twice as much in computer sales as he had in phone sales and earned a total of $70 in commission. Write a system of equations that could be used to determine the dollar amount of phone sales Kevin made and the dollar amount of computer sales he made. Define the variables that you use to write the system.

Answer 1

x the phones sales Kevin makes and y the computers sales Kevin makes.

`\left\{\begin{matrix}4x+5y=7000\\ -2x+y=0\end{matrix}\right`

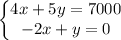
Explanation:

System Of Linear Equations

Two or more equations can be linked through common variables and each equation must be satisfied when the solution (if any) is found.

The general form of a system of two equations with two variables is

`\left\{\begin{matrix}ax+by=c\\ dx+ey=f\end{matrix}\right`

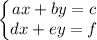
where x and y are the variables and the rest are constants. There are many methods to solve such systems, including Substitution, Elimination, Reduction, Graphics, Determinants, among many others

According to the conditions of the problem, Kevin earns a 4% commission on all phone sales he makes and earns a 5% commission on all computer sales. Let's call x the phone sales he makes and y his computer sales. Knowing the total commissions earned by Kevin are $70, we have

`0.04x+0.05y=70`

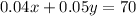
Recall 4%=0.04 and 5%=0.05

Multiplying by 100

`4x+5y=7000`

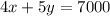
We also know Kevin had twice as much in computer sales as he had in phone sales. This is expressed as

`y=2x`

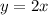
Rewriting

`-2x+y=0`

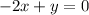
Putting both equations together, we form the system

`\left\{\begin{matrix}4x+5y=7000\\ -2x+y=0\end{matrix}\right`

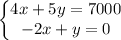
We are not required to solve the system, but you can find useful that

x=500, y=1000 is the solution