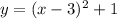Question

12

Which function is equivalent to y = x2 - 6x + 10?
A y = (x + 3)2 - 1
B y = (x - 3)2 + 1
c y = (x + 6)2 - 10
D y = (x - 6)2 + 10

Answer 1

B)
`y=(x-3)^2+1`

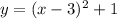
Explanation:

Given function:

`y=x^2-6x+10`

We need to find the equivalent function.

By looking at the choices, we know that we have to convert the given function into its vertex form.

We apply completing square method to do so.

We have

`y=x^2-6x+10`

First of all we make sure that the leading co-efficient is =1.

Since its already 1, so we move ahead to next term.

Isolating
`x^2` and
`x` terms on one side.

Subtracting both sides by 10.

`y-10=x^2-6x+10-10`

`y-10=x^2-6x`

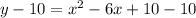
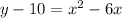
In order to make the right side a perfect square trinomial, we will take half of the co-efficient of
`x` term, square it and add it both sides side.

square of half of the co-efficient of
`x` term =
`((1)/(2)* 6)^2=3^2=9`

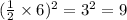
Adding 9 to both sides.

`y-10+9=x^2-6x+9`

`y-1=x^2-6x+9`

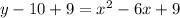
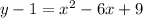
Since
`x^2-6x+9` is a perfect square of
`(x-3)`, so, we can write as:

`y-1=(x-3)^2`

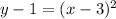
Adding 1 to both sides:

`y-1+1=(x-3)^2+1`

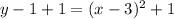
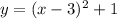`y=(x-3)^2+1` [Vertex form]

∴ Equivalent function
`y=(x-3)^2+1`