Answer:
The length of GH is 70 units.
Explanation:
It is given that, Q is circumcenter of triangle GHJ.
This means that, GQ = QH = JQ
given that, GQ = 15x - 23 and JQ = 9x + 1
thus,
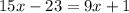
 , x = 4 units.
, x = 4 units.
Thus, GQ = QH = JQ = 9(4) + 1 = 37 units
QN is perpendicular to line GH.
Thus in right angled triangle QNH,
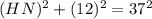
HN =
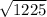 = 35 units.
= 35 units.
Triangles, QGN and QHN are congruent, thus GN = HN = 35 units
The length of GH = (2)(35) = 70 units.