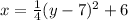Question

What is the equation of the parabola with vertex (6,7) and focus (7,7)?

Vertex: (6 , 7)
Focus: (7 , 7)​

Answer 1

Explanation:

If you plot these points on a coordinate plane, you see that they are on the same horizontal line, y = 7, with the focus 1 unit to the right of the vertex. This means that the parabola is a sideways opening parabola, to the right, to be more specific. That means that it has the basic vertex form

`4p(x-h)=(y-k)^2`

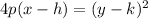
where p is the distance in units from the vertex to the focus, h is the first coordinate in the vertex, and k is the second coordinate in the vertex. For us, p = 1, h = 6, and k = 7. Now we will just fill the vertex form of the equation in with our values:

`4(x-6)=(y-7)^2`

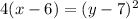
We will solve this for x now by dividing each side by 4 and adding over the 6:

`x=(1)/(4)(y-7)^2+6`