Question

11. Which description of transformations yields the

equation f(x) = |x +3| – 2 from its parent function
of f(x) = |x|?

Answer 1

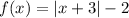`f(x)=|x+3|-2` includes: 1) a vertical shift downwards of "2" units, and 2) a horizontal shift to the left of 3 units.

Explanation:

Let's recall the rules for transforming functions via horizontal and vertical shifts of their graphs, and pay particular attention at the operations involved in the transformation of the function
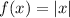`f(x)=|x|` leading to:
`f(x)=|x+3|-2`.

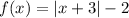We notice that the transformation added 3 units to the variable "x", and we also notice that there is a subtraction of 2 units to the full absolute value function. We therefore look for such changes in the list of vertical and horizontal shifts:

1) In order to shift the graph of a function vertically c units upwards, we must transform f (x) by adding c to it.

2) In order to shift the graph of a function vertically c units downwards, we must transform f (x) by subtracting c from it.

3) In order to shift the graph of a function horizontally c units to the right, we must transform the variable x by subtracting c from x.

4) In order to shift the graph of a function horizontally c units to the left, we must transform the variable x by adding c to x.

So we can conclude that the resulting function
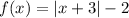`f(x)=|x+3|-2` includes: 1) a vertical shift downwards of "2" units, and 2) a horizontal shift to the left of 3 units.