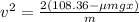Question

The 6 kg block is then released and accelerates

to the right, toward the 2 kg block. The
surface is rough and the coefficient of friction
between each block and the surface is 0.3 . The
two blocks collide, stick together, and move
to the right. Remember that the spring is not
attached to the 6 kg block.
Find the speed of the 6 kg block just before
it collides with the 2 kg block.
Answer in units of m/s

Answer 1

5.709 m/s

Step-by-step explanation:

Assuming compression of spring as 0.6m and spring constant of 602 N/m

The initial energy stored in the spring will be given by
`\frac {kx^(2)}{2}`

By substitution, the initial energy is \
`frac {602*0.6^(2)}{2}=108.36 J`

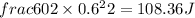
Kinetic energy of the 6 Kg block is given by subtracting energy lost due to friction from the initial stored energy hence

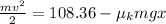`\frac {mv^(2)}{2}=108.36-\mu_k mgx` where m is mass, v is speed, g is acceleration due to gravity, x is the spring compression and
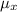`\mu_x` is the coefficient of friction

Making v the subject then

`v^(2)=\frac {2(108.36-\mu mgx)}{m}`

`v=\sqrt{\frac {2(108.36-\mu_x mgx)}{m}}= \sqrt {\frac {2(108.36-(0.3* 6* 9.8* 0.6))}{6}}\approx 5.709 m/s`