Answer:
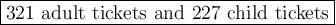
Explanation:
1. Set up the equations
Let a = the number of adult tickets
and c = the number of child tickets. Then
6.50a = revenue from adult tickets and
3.50c = revenue from child tickets
6.50a + 3.50c = total ticket revenue
You have a system of two equations:

2. Solve the equations
![\begin{array}{lrcll}(3) & c& = &548 - a&\text{Subtracted a from each side of (1)}\\ & 6.50a + 3.50(548 - a) & = & 2881 &\text{Substituted (3) into (2)}\\& 6.50a + 1918 - 3.50a & = & 2881 &\text{Distributed the 3.50}\\&3.00a + 1918 & = & 2881 &\text{Combined like terms}\\& 3.00a & = & 963 &\text{Simplified}\\& a & = & (963)/(3.00) &\text{Divided each side by 3.00}\end{array}]()

3. Check

OK.