Question

The points (-2, -3) and (5, 2) are the end points of the diameter of a circle. Find the length of the radius of the circle.

Answer 1

The length of the radius of the circle is 4.3 unit

Explanation:

Given as :

The end points of the diameter of a circle = (-2, -3) and (5, 2)

Let The point A = (-2, -3)

And The point B = (5, 2)

Now The measure of the diameter of the circle = The distance between points A and B

Or, Distance = Diameter =
`\sqrt{(y_2-y_1)^(2) + (x_2-x_1)^(2)  }`

Or, Diameter =
`\sqrt{(2-(-3))^(2) + (5-(-2))^(2)  }`

Or, Diameter =
`\sqrt{(5)^(2) + (7)^(2)  }`

Or, Diameter =
`√(74)`

∴ Diameter = 8.6 unit

So, The diameter of circle = 8.6 unit

Now, The radius of circle =
`(\textrm Diameter)/(2)`

Or, radius =
`(\textrm 8.6)/(2)`

∴ Radius = 4.3 unit

Hence The length of the radius of the circle is 4.3 unit Answer

Answer 2

The length of the radius of the circle = 4.30 units

Explanation:

Here, the endpoints of the diameter are given as A(-2,-3) and B(5,2).

Now, the given diameter is the segment AB.

DISTANCE FORMULA

It states that for two points P(a,b) and Q(c,d), the length of segment PQ is given as
`PQ = √((a-c)^2 + (d-b)^2)`

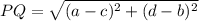
So, applying the formula here,

`AB = √((5-(-2))^2 + (2-(-3))^2)   = √((5+2)^2 + (2+3)^2)\\ =  √((7)^2 + (5)^2) = √(49 + 25 )  = √(74)  = 8.60`

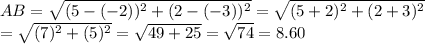
or, AB = 8.60 Units

So, the diameter of the circle = 8.6 units

Now, Diameter = 2 x Radius

So, R = D / 2

= 8.6 / 2 = 4. 3

or, Radius = 4.3 units

Hence, the length of the radius of the circle = 4.30 units