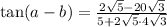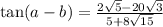Question

Find the exact value of the expression.
tan( sin−1 (2/3)− cos−1(1/7))

Answer 1

`\tan(a-b)=(2√(5)-20√(3))/(5+8√(15))`

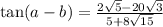
Explanation:

I'm going to use the following identity to help with the difference inside the tangent function there:

`\tan(a-b)=(\tan(a)-\tan(b))/(1+\tan(a)\tan(b))`

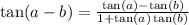
Let
`a=\sin^(-1)((2)/(3))`.

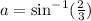With some restriction on
`a` this means:

`\sin(a)=(2)/(3)`

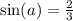
We need to find
`\tan(a)`.

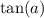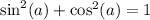`\sin^2(a)+\cos^2(a)=1` is a Pythagorean Identity I will use to find the cosine value and then I will use that the tangent function is the ratio of sine to cosine.

`((2)/(3))^2+\cos^2(a)=1`

`(4)/(9)+\cos^2(a)=1`

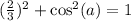
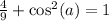
Subtract 4/9 on both sides:

`\cos^2(a)=(5)/(9)`

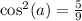
Take the square root of both sides:

`\cos(a)=\pm \sqrt{(5)/(9)}`

`\cos(a)=\pm (√(5))/(3)`

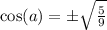
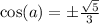
The cosine value is positive because
`a` is a number between
`-(\pi)/(2)` and
`(\pi)/(2)` because that is the restriction on sine inverse.

So we have
`\cos(a)=(√(5))/(3)`.

This means that
`\tan(a)=((2)/(3))/((√(5))/(3))`.

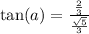Multiplying numerator and denominator by 3 gives us:

`\tan(a)=(2)/(√(5))`

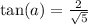
Rationalizing the denominator by multiplying top and bottom by square root of 5 gives us:

`\tan(a)=(2√(5))/(5)`

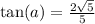
Let's continue on to letting
`b=\cos^(-1)((1)/(7))`.

Let's go ahead and say what the restrictions on
`b` are.

`b` is a number in between 0 and
`\pi`.

So anyways
`b=\cos^(-1)((1)/(7))` implies
`\cos(b)=(1)/(7)`.

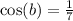Let's use the Pythagorean Identity again I mentioned from before to find the sine value of
`b`.

`\cos^2(b)+\sin^2(b)=1`

`((1)/(7))^2+\sin^2(b)=1`

`(1)/(49)+\sin^2(b)=1`

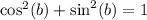
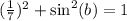
Subtract 1/49 on both sides:

`\sin^2(b)=(48)/(49)`

Take the square root of both sides:

`\sin(b)=\pm \sqrt{(48)/(49)`

`\sin(b)=\pm (√(48))/(7)`

`\sin(b)=\pm (√(16)√(3))/(7)`

`\sin(b)=\pm (4√(3))/(7)`

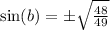
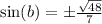
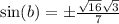
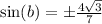
So since
`b` is a number between
`0` and
`\pi`, then sine of this value is positive.

This implies:

`\sin(b)=(4√(3))/(7)`

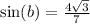
So
`\tan(b)=(\sin(b))/(\cos(b))=((4√(3))/(7))/((1)/(7))`.

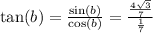Multiplying both top and bottom by 7 gives:

`(4√(3))/(1)= 4√(3)`.

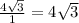Let's put everything back into the first mentioned identity.

`\tan(a-b)=(\tan(a)-\tan(b))/(1+\tan(a)\tan(b))`

`\tan(a-b)=((2√(5))/(5)-4√(3))/(1+(2√(5))/(5)\cdot 4√(3))`

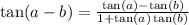
Let's clear the mini-fractions by multiply top and bottom by the least common multiple of the denominators of these mini-fractions. That is, we are multiplying top and bottom by 5:

`\tan(a-b)=(2 √(5)-20√(3))/(5+2√(5)\cdot 4√(3))`

`\tan(a-b)=(2√(5)-20√(3))/(5+8√(15))`