Answer:
5.80%
Explanation:
Given:
The probability of successful treatment of cancer is,
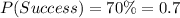
The probability of successful treatment in a given month is independent of the other month. So, probability of successful treatment for 'n' months in a row is given as:
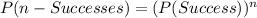
Plug in 8 for 'n' and determine the required probability. This gives,

Therefore, the probability that the treatment was successful 8 months in a row is 5.80% rounded to nearest tenth of a percent.