Question

At the movie theatre, child admission is $5.30 and adult admission is $9.70. On Wednesday, 156 tickets were sold for a total sales of $1077.60. How many adult tickets were sold that day?

Answer 1

The number of adult tickets are 57.

Explanation:

Given,

Total number of tickets = 156

Total money = $1077.60

Solution,

Let the number of adult be x and of child be y .

So, Total number of tickets = Number of adults + Number of child

`\therefore x+y = 156\ \ \ \ \ \ equation\ 1`

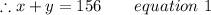
Now, according to question;

Total money =
`Number\ of\ adults* admission\ fee + Number\ of\ child* admission\ fee`

`\therefore x* 9.70+y* 5.30 = 1077.60\ \ \ \ \ \ equation\ 2`

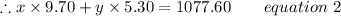
On multiplying by 10 on both side, we get;

`97x+53y=10776\ \ \ \ \ \ equation\ 3`

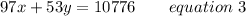
Now multiplying equation 1 by 53 then subtract it from equation 3, we get;

`(x+y)*53 = 156*53\\53x+53y=8268\\(97x+53y=10776)-(53x+53y=8268)\\44x=2508\\x=(2508)/(44) =57`

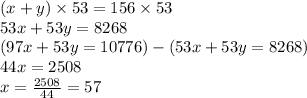
Since x is the number of adults,

Number of adults=57

Number of child = y = 156-57=99

Thus the number of adult tickets are 57.