Question

Need Answered ASAP

use the rational root theorem to list all possible rational roots of the polynomial equation
x^(3)-6x^(2)+4x+9=0
do not find the actual roots.

Answer 1

The possible rational roots are: +1, -1 ,+3, -3, +9, -9

Explanation:

The Rational Root Theorem tells us that the possible rational roots of the polynomial are given by all possible quotients formed by factors of the constant term of the polynomial (usually listed as last when written in standard form), divided by possible factors of the polynomial's leading coefficient. And also that we need to consider both the positive and negative forms of such quotients.

So we start noticing that since the leading term of this polynomial is
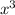`x^3`, the leading coefficient is "1", and therefore the list of factors for this is: +1, -1

On the other hand, the constant term of the polynomial is "9", and therefore its factors to consider are: +1, -1 ,+3, -3, +9, -9

Then the quotient of possible factors of the constant term, divided by possible factor of the leading coefficient gives us:

+1, -1 ,+3, -3, +9, -9

And therefore, this is the list of possible roots of the polynomial.