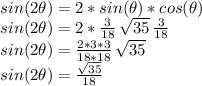Answer:
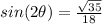
Explanation:
Recall the formula for the sine of the double angle:
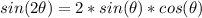
we know that
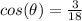 , and that
, and that
 is in the interval between 0 and 90 degrees, where both the functions sine and cosine are non-negative numbers. Based on such, we can find using the Pythagorean trigonometric property that relates sine and cosine of the same angle, what
is in the interval between 0 and 90 degrees, where both the functions sine and cosine are non-negative numbers. Based on such, we can find using the Pythagorean trigonometric property that relates sine and cosine of the same angle, what
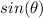 is:
is:
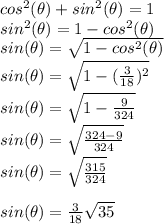
With this information, we can now complete the value of the sine of the double angle requested: