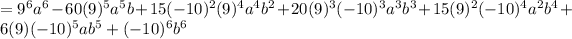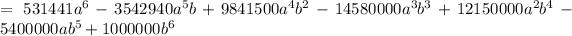Answer:
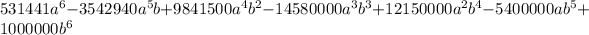
Explanation:
1 n=0
1 1 n=1
1 2 1 n=2
1 3 3 1 n=3
1 4 6 4 1 n=4
1 5 10 10 5 1 n=5
1 6 15 20 15 6 1 n=6
This is where n is the exponent in
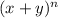 .
.
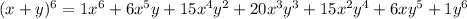
Now we want to expand:
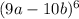 or we we can rewrite as
or we we can rewrite as
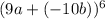 .
.
Let's replace
 with
with
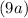 and
and
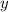 with
with
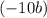 in the expansion:
in the expansion:
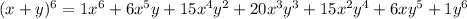
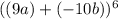
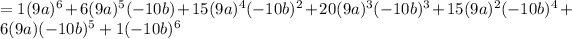
Let's simplify a bit: