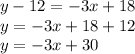Question

What is the equation for a line with points (6.12) and (3,21) in slope-intercept form

Answer 1

y = -3 x + 30

Explanation:

We need to find the slope and y-intercept of the line through the given points (6, 12) and (3, 21)

So we start by using the formula for the slope of the segment that joints any two points
`(x_1,y_1)` and
`(x_2,y_2)` which states:

slope =
`(y_2-y_1)/(x_2-x_1)`

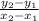
If we call
`(x_1,y_1)` = (6, 12) and
`(x_2,y_2)` = (3, 21),then the slope becomes:

`slope=(y_2-y_1)/(x_2-x_1)\\slope=(21-12)/(3-6)\\slope=(9)/(-3) \\slope=-3`

Now we use the slope "-3" in the point-slope form of a line with slope "-3) and going through the point (we take any one of the given points) : (6, 12):

`y-y_1=m\,(x-x_1)\\y-12=(-3)\,(x-6)\\y-12=-3x+18`

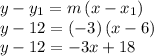
Now, to express the equation of the line in slope-intercept form, we simply solve for "y" in the above equation:

`y-12=-3x+18\\y=-3x+18+12\\y=-3x+30`