Question

23) A ball is launched into the air. The function h=-16 +126 gives the height of the

ball, in feet, at t seconds.
a. What is the maximum height the ball reaches?
b. About how long was the ball in the air? Round to the nearest hundredth if necessary.​

Answer 1

The equation is missing 't' terms. The correct equation is:

`h=-16t^2+126t`

Answer:

(a) 248.06 ft

(b) 7.875 s

Explanation:

Given:

Height of ball in air above ground is given as:

`h=-16t^2+126t`

(a)

At maximum height, the speed of the ball is 0 momentarily. Speed is nothing but rate of change of height which is the first derivative of height with time. Therefore,

At maximum height:

Speed = 0

`h'=0\\-16(2t)+126=0\\-32t+126=0\\32t=126\\t=(126)/(32)=3.9375\ s`

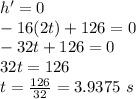
Now, maximum height is obtained by plugging in
`t=3.9375`. Thus,

`h_(max)=-16(3.9375)^2+126(3.9375)\\h_(max)=-248.0625+496.125=248.0625\ ft`

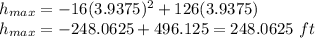
Therefore, the maximum height of the ball is 248.06 ft. (Rounded to nearest hundredth)

(b)

Now, total time of travel of the ball is the sum of time taken to reach maximum height and the time taken from maximum height to the bottom.

Also, time taken for upward journey would be same as that of downward journey. Therefore, total time taken is twice that of the upward journey.

We have,

Time to reach maximum height,
`t = 3.9375\ s`

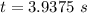
Therefore, total time the ball was in air =
`2(t)=2* 3.9375=7.875\ s`

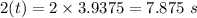
Hence, the ball was in the air for 7.88 s. (Rounded to nearest hundredth)